- Introduction
The science of physics is built fundamentally upon differential equations. Many of the most useful differential equations appearing in physics are of partial differential equations, known as math physical equations,
so that understanding the solutions that can arise and their interconnections has much to say about possible systems amenable to analyze physical problems.
In mathematics, a partial differential equation (PDE) is a differential equation that contains unknown multivariable functions and their partial derivatives. PDE are used to formulate problems involving functions of several variables,
and are either solved by computers, or used to create a computer model. A special case is ordinary differential equations (ODE), which deal with functions of a single variable and their derivatives.
PDE can be used to describe a wide variety of phenomena such as sound, heat, diffusion, electrostatics, electrodynamics, fluid dynamics, elasticity, gravitation and quantum mechanics.
These seemingly distinct physical phenomena can be formalised similarly in terms of PDEs. Just as ordinary differential equations often model one-dimensional dynamical systems, partial differential equations often model multidimensional systems.
Fractional differential equations (FDE) can describe the dynamics of several complex and nonlocal systems with memory. They arise in many scientific and engineering areas such as physics, chemistry, biology, biophysics, economics,
control theory, signal and image processing, etc. Particularly, nonlinear systems describing different phenomena can be modeled with fractional derivatives. Chaotic behavior has also been reported in some fractional models.
There exist theoretical results related to existence and uniqueness of solutions to initial and boundary value problems with fractional differential equations [1-5].
In this paper, it is shown that analytical solution of fractional differential equation are solved by MathHand.com. MathHand.com is the online math calculator, its former is SymbMath [6-7].
It is reviewed as Math Handbook Calculator [8].
The examples included fractional differential equation, fractional partial differential equation, fractional integral equation, equation of mixed Fractional differential and integral orders,
system of fractional differential equation, complex order differential equation, and a variable order differential equation.
By default, the Caputo definition of fractional calculus [9] is used here.
- Differential equation
By default, the unknown function is y(x) and its initial value is y(0). An independent variable is x for ordinary differential equation.
For a partial differential equation, the unknown function is y( ) and its two independent variables are x and t.
For a system of equations, two unknown functions are x(t) and y(t) with an independent variable t.
Table 1. Comparison of different orders
| Order | name | equation | y( ) | ds( ) | d( ) | ints( ) |
|---|
| 2 | second order | `(d^2 y)/dx^2 - 2y = exp(x)` | y(2,x) | ds(y,x,2) | d(y(x),x,2) | |
| 1.5 | 1.5 order | `d^1.5/dx^1.5 y - 2y = exp(x)` | y(1.5,x) | ds(y,x,1.5) | d(y(x),x,1.5) | |
| 1 | first order | `dy/dx - 2y = exp(x)` | y(1,x) | ds(y,x) | d(y(x),x) | |
| 0.5 | semi differential order | `d^0.5/dx^0.5 y - 2y = exp(x)` | y(0.5,x) | ds(y,x,0.5) | d(y(x),x,0.5) | |
| -0.5 | semi integral order | `d^-0.5/dx^-0.5 y - 2y = exp(x)` | y(-0.5,x) | ds(y,x,-0.5) | d(y(x),x,-0.5) | ints(y,x,0.5) |
| -1 | integral order | `int y\ dx-2y = exp(x)` | y(-1,x) | ds(y,x,-1) | d(y(x),x,-1) | ints(y,x) |
| -2 | double integral order | `int int y\ (dx)^2 - 2y = exp(x)` | y(-2,x) | ds(y,x,-2) | d(y(x),x,-2) | ints(y,x,2) |
| i | complex order | `(d^i y)/dx^i - 2y = exp(x)` | y(i,x) | ds(y,x,i) | d(y(x),x,i) | |
| cos(x) | variable order | `(d^cos(x) y)/dx^cos(x) - 2y = exp(x)` | y(cos(x),x) | ds(y,x,cos(x)) | d(y(x),x,cos(x)) | |
Input your equation into mathHand.com, click the "dsolve" button for solution, then click the "test" button to test its solution.
e.g.
input y(1,x) - 2y = exp(x) as first order differential equation for
`y^((1))(x) - 2y = exp(x)`
Or input the dsolve( ) function, click the "=" button for solution, then click the "test" button to test its solution.
e.g.
input dsolve( ds(y) - 2y = exp(x) ) for
dsolve `dy/dx - 2y = exp(x)`
Its solution is in Table 2.
Table 2. Comparison of differential equations with different orders
solution = general solution + parcular solution = gsolution( ) + psolution( )
The above table shows that parcular solutions of their differential equations are the same regardless with its order.
Solve ODE graphically
Some differential equations cannot be solved symbolly, but can be solved numerically and graphically by the ODE plot function odeplot( ), e.g. input
sin(x)-cos(y) for y' = sin(x)-cos(y), then tick the y'= or y"= checkbox to solve first or second order differential eq.
by default it is first order ODE.
y''=y'-y for second order ODE
- Partial differential equation
Input your PDE equation, click the PDE button, then click the plot2D button
to show its curve graph where you can change a time t value, or click the plot3D button
to show its 3D graph where you can spin graph.
Laplace equation
Study the balance or stability process of gravitational field, static force field,
magnetic field and some physical phenomena (such as vibration, heat conduction, diffusion),
usually get elliptic equation, the most typical equation is Laplace equation
Δ y = 0
Where Δ is the Laplace operator.
The Laplace operator in two dimensions x and z is
`Δ y = (d^2y)/(dx^2)+(d^2y)/(dz^2)`
The Laplace equation in two dimensions x and z is
`Δ y = (d^2y)/(dx^2)+(d^2y)/(dz^2)=0`
When the area is a circle or a sphere, it is more convenient to use polar coordinates ( r ) or spherical coordinates ( r , θ ) , respectively .
The polar coordinate form of Δ y = 0 is
`r^2*(d^2 y)/(dr^2)+r*dy/(dr) = 0`
Poisson equation
Δ y = ρ
Where ρ is a known function, Δ is the Laplace operator.
e.g. Poisson integral of the solution to the Dirichlet problem of a circle.
`r^2*(d^2 y)/(dr^2)+r*dy/(dr) = 1`
A first order differential time equation
Input ds(y,t,1) = ds(y,x,2)-ds(y,x)-exp(x)-exp(t) as a first order partial differential time t in the left hand side of the equation,
`(dy)/dt - (d^2y)/dx^2-dy/dx-exp(t)-exp(x)`
Heat conduction equation and diffusion equation
The heat conduction equation describes the physical laws of heat conduction and molecular diffusion .
In a heat conducting material, the temperature y obeys the diffusion equation.
The general form of the heat conduction equation is
`dy/dt-a^2*Δy = f(t,x)`
Where Δ is the Laplace operator, f(t,x) is a continuous and bounded function.
e.g. a diffusion equation in one dimemtion:
`(dy)/dt - a^2*(d^2y)/dx^2 =0`
e.g. a diffusion equation in 2 dimemtions:
`(dy)/dt = (d^2y)/dx^2 + (d^2y)/(du^2) `
e.g. The polar coordinate form of dy/dt - Δ y = 0 is
`(dy)/(dmu)-r^2*(d^2 y)/(dr^2)-r*dy/(dr) = 0`
e.g. a spherical diffusion equation:
`(dy)/dt = (d^2y)/(dx^2) + 1/x*dy/(dx) `
e.g. a diffusion equation in 3 dimemtions:
`(dy)/(dt) = (d^2y)/dx^2 + (d^2y)/(du^2) + (d^2y)/(dv^2) `
A second order differential time equation,
Input ds(y,t,2) - ds(y,x,2)-ds(y,x)-exp(x)-exp(t) as second order partial differential time t in the left hand side of the equation,
`(d^2y)/dt^2 - (d^2y)/dx^2-dy/dx-exp(t)-exp(x)`
Wave equation
The laws of motion of many objects can be described by wave equations .
For example, string vibration can be described by one-dimensional wave equation; membrane vibration can be described by two-dimensional wave equation; acoustic wave and electromagnetic wave oscillation can be described by three-dimensional wave equation .
Study the wave equation of the form
`(d^2y)/dt^2-a^2 Δ y = f(t,x,v,z)`
Where f( x , v , z , t ) is a known function .
Solution to the Cauchy Problem of Homogeneous Equation
e.g. a wave equation in one dimemtion:
`(d^2y)/dt^2 - a^2 * (d^2y)/dx^2 =0 `
e.g. a wave equation in two dimemtions. The continuous solution of the two-dimensional Laplace equation is called the harmonic function
`(d^2y)/(dt^2) - a^2 * ((d^2y)/dx^2 + (d^2y)/(dz^2)) =0 `
e.g. a wave equation in three dimemtions:
`(d^2y)/(dt^2) - a^2 * ((d^2y)/dx^2 + (d^2y)/(dv^2) + (d^2y)/(dz^2))=0 `
- Integral equation
Integral equation is equation with the -1 differential order. e.g.
Input ds(y,x, -1) - 2y = exp(x) for
`d^-1/dx^-1 y - 2y = exp(x)`
Intput integrates(y) = 2y for
`int y` dx - 2y = exp(x)
Its solution is in Table 2. Integral equation can be converted to differential equation by differentiating both sides, and then it is solved.
Double Integral equation
Double integral equation is equation with the -2 differential order. e.g.
Intput ds(y,x,-2) - 2y = exp(x) for
`int int y` `(dx)^2` - 2y = exp(x)
Its solution is in Table 2.
- Fractional differential equation
Differential and integral equations can be extend to fractional differential and integral equations by fractional order of fractional calculus. e.g.
Input ds(y,x,0.5) = 2y as semi differential equation with the 0.5 differential order for
`d^0.5/dx^0.5 y = 2y`
Solve (fractional) differential equation for y by dsolve( ), e.g.
dsolve( `d^0.5/dx^0.5 y = 2y` )
Its solution is in Table 2. Property of a fractional differential equation is the same as a differential equation:
Solution of linear fractional differential equation = general solution + parcular solution = gsolution( ) + psolution( )
It is similar to linear differential equation, so method to solve fractional differential equation is similar to differential equation [3-5].
- Fractional partial differential equation
When PDE is extended to the fractional time, the time order in PDE is changed to frational time order.
Consider a time fractional partial differential equation with fractional order differential time.
The above diffusion equations and wave equations can be changed to fractional diffusion equations and wave equations
by change of the time order to fractional order, e.g. 0.5 order.
Heat conduction equation with fractional time order
The general form of the heat conduction equation is
`(d^0.5y)/dt^0.5-a^2*Δ y = f(t,x)`
Where Δ is Laplace operator, f(t,x) is a continuous and bounded function.
The heat conduction equation describes the physical laws of heat conduction and molecular diffusion .
e.g. a diffusion equation in one dimemtion with fractional time order:
`(d^0.5y)/dt^0.5 - a^2* (d^2y)/dx^2 =0`
Input ds(y,t,0.5)=ds(y,x,2)-ds(y,x)-exp(x)-exp(t) as semi partial differential time t in the left hand side of the equation, e.g. when a=1, f(t,x)=exp(t)+exp(x), the equation becomes
`(d^0.5y)/dt^0.5 = (d^2y)/dx^2-exp(x)-exp(t)`
e.g. a diffusion equation in two dimemtions with fractional time order:
`(d^0.5y)/dt^0.5 = (d^2y)/dx^2+(d^2y)/(dz^2)-exp(x)`
- Fractional integral equation
Integral equation is extend to fractional integral equation by minus fractional order. e.g.
Input ds(y,x, -0.5) - 2y = exp(x) as semi integral equation with the -0.5 differential order for
`d^-0.5/dx^-0.5 y - 2y = exp(x)`
Intput integrates(y,x,0.5) - 2y = exp(x) for
`int y` `(dx)^0.5` - 2y = exp(x)
Its solution is in Table 2. By default, the Caputo definition of fractional calculus is used by dsolve( ). If you want to use the Riemann defintion, use the Laplace transform solver lasolve( ).
Difference between Caputo definition and the Riemann-Liouville (R-L) definition are in section 6 of fractional calculus [8]. e.g.
dsolve(y(-0.5,x)=1) give zero.
lasolve(y(-0.5,x)=1) give nonzero.
Integral equation can be converted to differential equation by differentiating both sides. In the same way, fractional integral equation aslo can be
converted to fractional differential equation, then it is solved.
- Equation of mixed Fractional differential and integral orders
A mix of differential and integral equation, e.g.
`d^(pi)/dx^(pi) y - int y(x) (dx)^pi` = exp(x)
- System of Fractional differential equations
By default, the unknown function are x(t) and y(t) and their variable is t, their initial value are x(0) and y(0) in a system of differential equations.
dsolve(x(1,t)=x-t, y(1,t)=t-x)
A system of differential equations is extend to system of fractional differential equation by fractional order. e.g.
`(d^0.5x)/dt^0.5 = 2x, (d^0.5y)/dt^0.5 = x+y`
- Complex order differential equation
Differential equation is extend to complex order differential equation by extension of order to complex number. e.g.
Input ds(y,x,i) - 2y -exp(x) = 0 as complex order differential equation for
`(d^(i)y)/dx^(i)- 2y - exp(x) = 0`
Its solution is in Table 2.
- Variable order differential equation
When the order is variable, it is a variable order differential equation. e.g. the order is continually changing between 1 and -1 in the cos(x) order differential equation:
`(d^cos(x) y)/dx^cos(x) - 2y = exp(x)`
Its solution is in Table 2, where `E_cos(x)( x )` is Mittag-Leffler function.
The order change is similar to a change of the n-order fractional derivative `d^n/dx^n x` in below animation Fig.1.
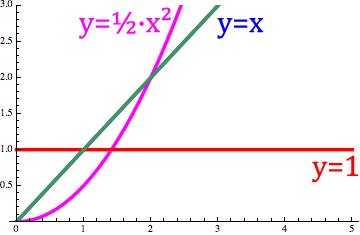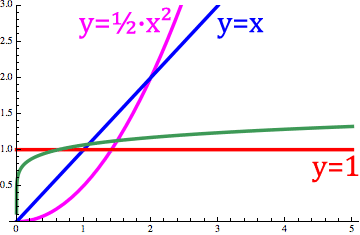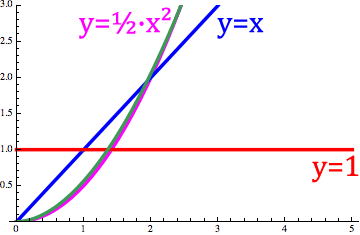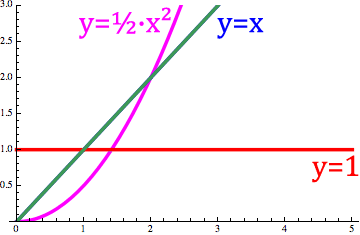
Fig. 1. Animation of the order changes between 1 and -1.
- Comparison of differential equations with different orders
It is interesting to compare differential equations with different orders in Table 2.
It is shown in Table 2 that all of solutions of the constant order equations are in the same format exp(k x). When the order of differential equations decreased from 2 to 0.5, their general solution increased from exp(sqrt(2)*x) to exp(4x).
When the order of integral equations decreased from -0.5 to -2, their general solution also increased from exp(1/4 x) to exp(1/sqrt(2) x), but all of their parcular solutions are unchanged.
- Test solution
Test solution for (fractional) differential equation by the solutions back into equation to check if result is zero. There sre three ways to check solutions:
- Click the "test" button to test solution, if it is not 0, then click the plot2D button to show a line of 0.
- Use the test( ) to test solution by test(solution, equation), e.g.
`test( exp(4x), d^0.5/dx^0.5 y = 2y )`
f:= 2y+1, eq:=y'-f=0, s:=dsolve(eq), test(s, eq)
f:= 2y+1, eq:=ds(y,x,0.5)-f=0, s:=dsolve(eq), test(s, eq)
- the ntest( ) is numeric test to put a random number into independent variable back to the equation by ntest(solution, equation).
- Conclusion
An overview of the solution methods for differential equations in the MathHandbook function dsolve is presented.
More examples are available on the documentation page [10], and
the examples included the differential equations [11] which other software cannot, e.g. Wolfram Bugs [12].
We hope that the examples and ideas outlined in this paper will be useful for
elementary and advanced courses on differential equations, as well as for
solving differential equations which occur in research and design problems in practice.
The integration of AI into math education has opened new horizons for personalized, interactive, and effective learning. The AI tool empower students to conquer math challenges with confidence. As technology evolves, the future of math education looks bright, promising a world where every student can excel in mathematics with the help of AI.
- References
- K.B. Oldham, J. Spanier, The Fractional Calculus, Academic Press, New York, London (1974).
- B. Ross. fractional calculus and its applications. Springer, Berlin, Heidelberg, 1975.
- K.B. Miller, B. Ross, An Introduction to the Fractional Calculus and Fractional Differential Equations, Wiley, New York (1993).
- I. Podlubny, Fractional Differential Equations, Academic Press, New York (1999).
- Y. Hu, Y. Luo, Z. Lu, Analytical solution of the linear fractional differential equation by Adomian decomposition method, Volume 215, Issue 1, 15 May 2008, p 220-229.
- W. Huang, SymbMath: A Program for Symbolic Mathematics, Int. J. Math. Edu. Sci. Technol., 1992, 23(1), 160-165.
- W. Huang, SymbMath Update to Version 2.0, Abs. Amer. Math. Soc., 1992, 13(6), 535.
- Math Handbook Calculator, https://blog.actorsfit.com/a?ID=00550-3e2ed6ca-f8f1-49ba-aafd-2b44cee0ab44, last access 21//07/2021.
- Fractional calculus , http://drhuang.com/science/mathematics/fractional_calculus/, last accessed 21//07/2021.
- Examples of Fractional Calculus Computer Algebra System, http://drhuang.com/index/example/, last accessed 21//07/2021.
- Special differential equation, https://jingyan.baidu.com/article/19020a0a6bb358529d284293.html, last accessed 21//07/2021.
- Wolfram bugs, http://drhuang.com/index/bugs/, last accessed 21//07/2021.
 +
+  +
+  +
+  =
= 
 +
+  +
+  +
+  =
= 
