|
|
|
N.B. A detailed on-line essay by S. Finch was the starting point for this entry.
An Infinite Sequence of Positive Integers ![]() satisfying
satisfying
| (1) |
 |
(2) |
| (3) |
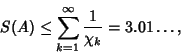 |
(4) |
See also B2-Sequence, Mian-Chowla Sequence
References
Abbott, H. L. ``On Sum-Free Sequences.'' Acta Arith. 48, 93-96, 1987.
Erdös, P. ``Remarks on Number Theory III. Some Problems in Additive Number Theory.'' Mat. Lapok 13,
28-38, 1962.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/erdos/erdos.html
Guy, R. K. ``
Levine, E. and O'Sullivan, J. ``An Upper Estimate for the Reciprocal Sum of a Sum-Free Sequence.'' Acta
Arith. 34, 9-24, 1977.
Zhang, Z. X. ``A Sum-Free Sequence with Larger Reciprocal Sum.'' Unpublished manuscript, 1992.
![]() -Sequences.'' §E28 in Unsolved Problems in Number Theory, 2nd ed.
New York: Springer-Verlag, pp. 228-229, 1994.
-Sequences.'' §E28 in Unsolved Problems in Number Theory, 2nd ed.
New York: Springer-Verlag, pp. 228-229, 1994.