|
|
|
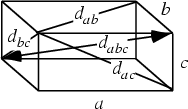
A Rectangular Parallelepiped (``Brick'') with integral edges ![]() and face diagonals
and face diagonals
![]() given by
given by
| (1) | |||
| (2) | |||
| (3) |
Euler ![]() found the smallest solution, which has sides
found the smallest solution, which has sides ![]() ,
, ![]() , and
, and ![]() and face
Diagonals
and face
Diagonals ![]() ,
, ![]() , and
, and ![]() . Kraitchik gave 257
cuboids with the Odd edge less than 1 million (Guy 1994, p. 174). F. Helenius has compiled a list of the 5003
smallest (measured by the longest edge) Euler bricks. The first few are (240, 117, 44), (275, 252, 240), (693, 480,
140), (720, 132, 85), (792, 231, 160), ... (Sloane's
A031173,
A031174,
and A031175). Parametric solutions for Euler
bricks are also known.
. Kraitchik gave 257
cuboids with the Odd edge less than 1 million (Guy 1994, p. 174). F. Helenius has compiled a list of the 5003
smallest (measured by the longest edge) Euler bricks. The first few are (240, 117, 44), (275, 252, 240), (693, 480,
140), (720, 132, 85), (792, 231, 160), ... (Sloane's
A031173,
A031174,
and A031175). Parametric solutions for Euler
bricks are also known.
No solution is known in which the oblique Space Diagonal
| (4) |
| (5) | |||
| (6) | |||
| (7) | |||
| (8) |
See also Cuboid, Cyclic Quadrilateral, Diagonal (Polyhedron), Parallelepiped, Pythagorean Quadruple
References
Guy, R. K. ``Is There a Perfect Cuboid? Four Squares whose Sums in Pairs are Square. Four Squares whose
Differences are Square.'' §D18 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 173-181, 1994.
Helenius, F. First 1000 Primitive Euler Bricks. notebooks/EulerBricks.dat.
Leech, J. ``The Rational Cuboid Revisited.'' Amer. Math. Monthly 84, 518-533, 1977. Erratum in
Amer. Math. Monthly 85, 472, 1978.
Sloane, N. J. A. Sequences
A031173,
A031174, and
A031175
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
Rathbun, R. L. Personal communication, 1996.
Spohn, W. G. ``On the Integral Cuboid.'' Amer. Math. Monthly 79, 57-59, 1972.
Spohn, W. G. ``On the Derived Cuboid.'' Canad. Math. Bull. 17, 575-577, 1974.
Wells, D. G. The Penguin Dictionary of Curious and Interesting Numbers. London: Penguin, p. 127, 1986.
|
|
|
© 1996-9 Eric W. Weisstein