|
|
|
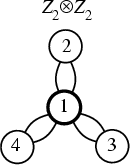
One of the two groups of Order 4. The name of this group derives from the fact that it is a
Direct Product of two ![]() Subgroups. Like the group
Subgroups. Like the group ![]() ,
,
![]() is an Abelian Group. Unlike
is an Abelian Group. Unlike ![]() , however, it is not Cyclic. In addition to
satisfying
, however, it is not Cyclic. In addition to
satisfying ![]() for each element
for each element ![]() , it also satisfies
, it also satisfies ![]() , where 1 is the Identity Element.
Examples of the
, where 1 is the Identity Element.
Examples of the
![]() group include the Viergruppe, Point Groups
group include the Viergruppe, Point Groups ![]() ,
, ![]() , and
, and ![]() , and
the Modulo Multiplication Groups
, and
the Modulo Multiplication Groups ![]() and
and ![]() . That
. That ![]() , the Residue
Classes prime to 8 given by
, the Residue
Classes prime to 8 given by
![]() , are a group of type
, are a group of type
![]() can be shown by verifying
that
can be shown by verifying
that
| (1) |
| (2) |
The Cycle Graph is shown above, and the multiplication table for the
![]() group is given below.
group is given below.
|
|
1 | |||
| 1 | 1 | |||
| 1 | ||||
| 1 | ||||
| 1 |
The Conjugacy Classes are ![]() ,
, ![]() ,
,
| (3) | |||
| (4) | |||
| (5) |
| (6) | |||
| (7) |
Now explicitly consider the elements of the ![]() Point Group.
Point Group.
In terms of the Viergruppe elements
A reducible representation using 2-D Real Matrices is
| (8) | |||
![$\displaystyle \left[\begin{array}{cc}-1 & 0 \\ 0 & -1 \end{array}\right]$](f_1203.gif) |
(9) | ||
| (10) | |||
![$\displaystyle \left[\begin{array}{cc}0 & -1 \\ -1 & 0 \end{array}\right].$](f_1205.gif) |
(11) |
![$\displaystyle E = E = \left[\begin{array}{ccc}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]$](f_1209.gif) |
(12) | ||
![$\displaystyle R_x(\pi) = \sigma_v = \left[\begin{array}{ccc}1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{array}\right]$](f_1210.gif) |
(13) | ||
![$\displaystyle R_z(\pi) = C_2 = \left[\begin{array}{ccc}-1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1\end{array}\right]$](f_1211.gif) |
(14) | ||
![$\displaystyle R_y(\pi) = \sigma_v' = \left[\begin{array}{ccc}-1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right].$](f_1212.gif) |
(15) |
| (16) |
| (17) |
| 1 | ||||
| 1 | 1 | 1 | 1 | |
| 1 | 1 | |||
| 1 | 1 | |||
| 1 | 1 |
These can be put into a more familiar form by switching ![]() and
and ![]() , giving the Character Table
, giving the Character Table
| 1 | ||||
| 1 | 1 | |||
| 1 | 1 | |||
| 1 | 1 | 1 | 1 | |
| 1 | 1 |
The matrices corresponding to this representation are now
![$\displaystyle \left[\begin{array}{cccc}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{array}\right]$](f_1155.gif) |
(18) | ||
![$\displaystyle \left[\begin{array}{cccc}-1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]$](f_1221.gif) |
(19) | ||
![$\displaystyle \left[\begin{array}{cccc}1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & -1 \end{array}\right]$](f_1223.gif) |
(20) | ||
![$\displaystyle \left[\begin{array}{cccc}-1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & -1 \end{array}\right],$](f_1225.gif) |
(21) |
See also Finite Group Z4
|
|
|
© 1996-9 Eric W. Weisstein