|
|
|
Any Composite Number ![]() with
with ![]() for all Prime Divisors
for all Prime Divisors ![]() of
of ![]() .
. ![]() is a Giuga
number Iff
is a Giuga
number Iff
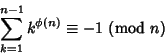
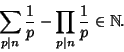
244197000982499715087866346, 554079914617070801288578559178(8 factors), ... (Sloane's A007850).
It is not known if there are an infinite number of Giuga numbers. All the above numbers have sum minus product equal to 1, and any Giuga number of higher order must have at least 59 factors. The smallest Odd Giuga number must have at least nine Prime factors.
See also Argoh's Conjecture, Bernoulli Number, Totient Function
References
Borwein, D.; Borwein, J. M.; Borwein, P. B.; and Girgensohn, R. ``Giuga's Conjecture on Primality.''
Amer. Math. Monthly 103, 40-50, 1996.
Sloane, N. J. A. Sequence
A007850
in ``The On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.