Let 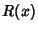 be the revenue for a production
be the revenue for a production 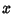 ,
, 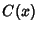 the cost, and
the cost, and 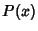 the profit.
Then
the profit.
Then
and the marginal profit for the 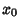 th unit is defined by
th unit is defined by
where 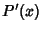 ,
, 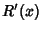 , and
, and 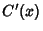 are the Derivatives
of
are the Derivatives
of 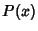 ,
, 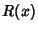 , and
, and 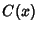 , respectively.
, respectively.
See also Derivative
© 1996-9 Eric W. Weisstein
1999-05-26
![]() be the revenue for a production
be the revenue for a production ![]() ,
, ![]() the cost, and
the cost, and ![]() the profit.
Then
the profit.
Then