|
|
|
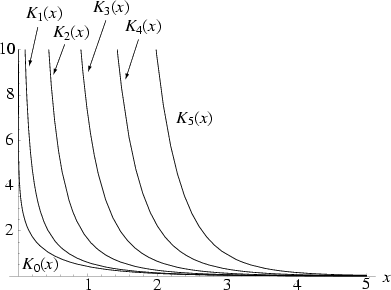
The function ![]() which is one of the solutions to the Modified Bessel Differential Equation. The above plot
shows
which is one of the solutions to the Modified Bessel Differential Equation. The above plot
shows ![]() for
for ![]() , 2, ..., 5.
, 2, ..., 5. ![]() is closely related to the Modified Bessel Function of the First
Kind
is closely related to the Modified Bessel Function of the First
Kind ![]() and Hankel Function
and Hankel Function ![]() ,
,
| (1) | |||
| (2) | |||
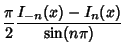 |
(3) |
|
|
|
![$ +(-1)^n {\textstyle{1\over 2}}({\textstyle{1\over 2}}z)^n \sum_{k=0}^\infty [\psi(k+1)+\psi(n+k+1)]{({\textstyle{1\over 4}}z^2)^k\over k!(n+k)!},\quad$](m_1408.gif)
|
(4) |
| (5) |
| (6) |
| (7) |
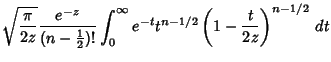 |
(8) | ||
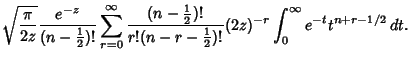 |
(9) |
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Modified Bessel Functions
Arfken, G. ``Modified Bessel Functions,
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Modified Bessel Functions of Integral Order''
and ``Bessel Functions of Fractional Order, Airy Functions, Spherical Bessel Functions.'' §6.6 and 6.7 in
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England:
Cambridge University Press, pp. 229-245, 1992.
Spanier, J. and Oldham, K. B. ``The Basset
Watson, G. N. A Treatise on the Theory of Bessel Functions, 2nd ed. Cambridge, England: Cambridge University
Press, 1966.
![]() and
and ![]() .''
§9.6 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 374-377, 1972.
.''
§9.6 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 374-377, 1972.
![]() and
and ![]() .'' §11.5 in
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 610-616, 1985.
.'' §11.5 in
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 610-616, 1985.
![]() .''
Ch. 51 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 499-507, 1987.
.''
Ch. 51 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 499-507, 1987.
|
|
|
© 1996-9 Eric W. Weisstein