|
|
|
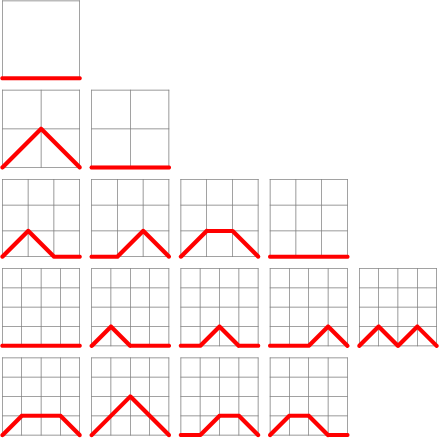
The Motzkin numbers enumerate various combinatorial objects. Donaghey and Shapiro (1977) give 14 different manifestations of
these numbers. In particular, they give the number of paths from (0, 0) to (![]() , 0) which never dip below
, 0) which never dip below ![]() and are made
up only of the steps (1, 0), (1, 1), and (1,
and are made
up only of the steps (1, 0), (1, 1), and (1, ![]() ), i.e.,
), i.e., ![]() ,
, ![]() , and
, and ![]() . The first are 1, 2, 4,
9, 21, 51, ... (Sloane's A001006). The Motzkin number Generating Function
. The first are 1, 2, 4,
9, 21, 51, ... (Sloane's A001006). The Motzkin number Generating Function ![]() satisfies
satisfies
| (1) |
| (2) |
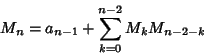 |
(3) |
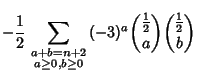 |
(4) | ||
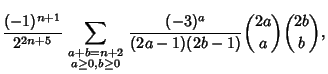 |
|||
| (5) |
See also Catalan Number, King Walk, Schröder Number
References
Barcucci, E.; Pinzani, R.; and Sprugnoli, R. ``The Motzkin Family.'' Pure Math. Appl. Ser. A 2, 249-279, 1991.
Donaghey, R. ``Restricted Plane Tree Representations of Four Motzkin-Catalan Equations.'' J. Combin. Th. Ser. B 22,
114-121, 1977.
Donaghey, R. and Shapiro, L. W. ``Motzkin Numbers.'' J. Combin. Th. Ser. A 23, 291-301, 1977.
Kuznetsov, A.; Pak, I.; and Postnikov, A. ``Trees Associated with the Motzkin Numbers.'' J. Combin. Th. Ser. A 76, 145-147, 1996.
Motzkin, T. ``Relations Between Hypersurface Cross Ratios, and a Combinatorial Formula for Partitions of a Polygon, for Permanent
Preponderance, and for Nonassociative Products.'' Bull. Amer. Math. Soc. 54, 352-360, 1948.
Sloane, N. J. A. Sequence
A001006/M1184
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
|
|
|
© 1996-9 Eric W. Weisstein