|
|
|
An interpolation Algorithm which proceeds by first fitting a Polynomial ![]() of degree 0 through the points
of degree 0 through the points
![]() for
for ![]() ...,
..., ![]() , i.e.,
, i.e., ![]() . A second iteration is then performed in which
. A second iteration is then performed in which ![]() is fit through
pairs of points, yielding
is fit through
pairs of points, yielding ![]() ,
, ![]() , .... The procedure is repeated, generating a ``pyramid'' of approximations
until the final result is reached
, .... The procedure is repeated, generating a ``pyramid'' of approximations
until the final result is reached
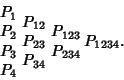
See also Bulirsch-Stoer Algorithm