Newton's Forward Difference Formula

A Finite Difference identity giving an interpolated value between tabulated points $\{f_p\}$ in terms of the first value $f_0$ and the Powers of the Forward Difference $\Delta$. For $a\in[0,1]$, the formula states

$$f_a=f_0+a\Delta+{\textstyle{1\over 2!}}a(a-1)\Delta^2+{\textstyle{1\over 3!}}a(a-1)(a-2)\Delta^3+\ldots.$$

When written in the form

$$f(x+a)=\sum_{n=0}^\infty {(a)_n \Delta^n f(x)\over n!}$$

with $(a)_n$ the Pochhammer Symbol, the formula looks suspiciously like a finite analog of a Taylor Series expansion. This correspondence was one of the motivating forces for the development of Umbral Calculus.

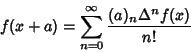
The Derivative of Newton's forward difference formula gives Markoff's Formulas.

See also Finite Difference, Markoff's Formulas, Newton's Backward Difference Formula, Newton's Divided Difference Interpolation Formula

References

Abramowitz, M. and Stegun, C. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 880, 1972.

Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 432, 1987.