|
|
|
Orthogonal polynomials are classes of Polynomials ![]() over a range
over a range ![]() which obey an
Orthogonality relation
which obey an
Orthogonality relation
| (1) |
Orthogonal polynomials have very useful properties in the solution of mathematical and physical problems. Just as Fourier Series provide a convenient method of expanding a periodic function in a series of linearly independent terms, orthogonal polynomials provide a natural way to solve, expand, and interpret solutions to many types of important Differential Equations. Orthogonal polynomials are especially easy to generate using Gram-Schmidt Orthonormalization. Abramowitz and Stegun (1972, pp. 774-775) give a table of common orthogonal polynomials.
In the above table, the normalization constant is the value of
| (2) |
| (3) |
The Roots of orthogonal polynomials possess many rather surprising and useful properties. For instance, let
![]() be the Roots of the
be the Roots of the ![]() with
with ![]() and
and ![]() . Then each interval
. Then each interval
![]() for
for ![]() , 1, ...,
, 1, ..., ![]() contains exactly one Root of
contains exactly one Root of ![]() . Between two Roots of
. Between two Roots of
![]() there is at least one Root of
there is at least one Root of ![]() for
for ![]() .
.
Let ![]() be an arbitrary Real constant, then the Polynomial
be an arbitrary Real constant, then the Polynomial
| (4) |
| (5) |
The following decomposition into partial fractions holds
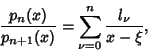 |
(6) |
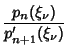 |
|||
![$\displaystyle {p_{n+1}'(\xi_\nu)p_n(\xi_\nu)-p_n'(\xi_\nu)'p_{n+1}(\xi_\nu)\over[p_{n+1}'(\xi_\nu)]^2}>0.$](o_982.gif) |
(7) |
Another interesting property is obtained by letting ![]() be the orthonormal set of Polynomials
associated with the distribution
be the orthonormal set of Polynomials
associated with the distribution ![]() on
on ![]() . Then the Convergents
. Then the Convergents ![]() of the
Continued Fraction
of the
Continued Fraction
| (8) |
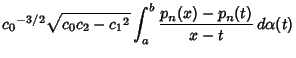 |
(9) | ||
| (10) |
| (11) |
See also Chebyshev Polynomial of the First Kind, Chebyshev Polynomial of the Second Kind, Gram-Schmidt Orthonormalization, Hermite Polynomial, Jacobi Polynomial, Krawtchouk Polynomial, Laguerre Polynomial, Legendre Polynomial, Orthogonal Functions, Spherical Harmonic, Ultraspherical Polynomial, Zernike Polynomial
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Orthogonal Polynomials.'' Ch. 22 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 771-802, 1972.
Arfken, G. ``Orthogonal Polynomials.'' Mathematical Methods for Physicists, 3rd ed.
Orlando, FL: Academic Press, pp. 520-521, 1985.
Iyanaga, S. and Kawada, Y. (Eds.). ``Systems of Orthogonal Functions.'' Appendix A, Table 20 in
Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 1477, 1980.
Nikiforov, A. F.; Uvarov, V. B.; and Suslov, S. S.
Classical Orthogonal Polynomials of a Discrete Variable. New York: Springer-Verlag, 1992.
Sansone, G. Orthogonal Functions. New York: Dover, 1991.
Szegö, G. Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., pp. 44-47 and
54-55, 1975.
|
|
|
© 1996-9 Eric W. Weisstein