|
|
|
A symbol used to describe Uniform Polyhedra. For example, the Wythoff symbol for the
Tetrahedron is ![]() . There are three types of Wythoff symbols
. There are three types of Wythoff symbols ![]() ,
, ![]() and
and ![]() ,
and one exceptional symbol
,
and one exceptional symbol
![]() used for the Great Dirhombicosidodecahedron. Some
special cases in terms of Schläfli Symbols are
used for the Great Dirhombicosidodecahedron. Some
special cases in terms of Schläfli Symbols are
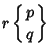 |
|||
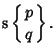 |
See also Uniform Polyhedron
References
Har'El, Z. ``Uniform Solution for Uniform Polyhedra.'' Geometriae Dedicata 47, 57-110, 1993.